Friedrich Walzel, Alice Requier, Kevin Boschi, Jean Farago, Philippe Fuchs, Fabrice Thalmann, Wiebke Drenckhan, Pierre Muller, and Thierry Charitat
Phys. Rev. E 106, 014803
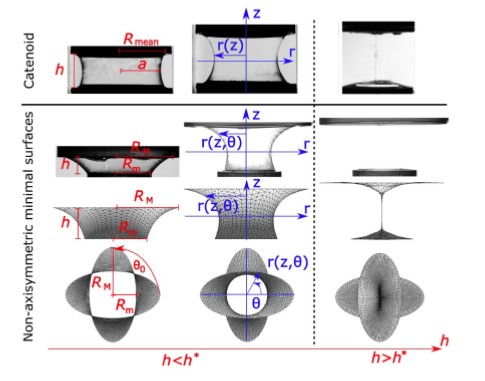
Minimal surface problems arise naturally in many soft matter systems whose free energies are dominated by surface or interface energies. Of particular interest are the shapes, stability, and mechanical stresses of minimal surfaces spanning specific geometric boundaries. The “catenoid” is the best-known example where an analytical solution is known which describes the form and stability of a minimal surface held between two parallel, concentric circular frames. Here we extend this problem to nonaxisymmetric, parallel frame shapes of different orientations by developing a perturbation approach around the known catenoid solution. We show that the predictions of the perturbation theory are in good agreement with experiments on soap films and finite element simulations (Surface Evolver). Combining theory, experiment, and simulation, we analyze in depth how the shapes, stability, and mechanical properties of the minimal surfaces depend on the type and orientation of elliptic and three-leaf clover shaped frames. In the limit of perfectly aligned nonaxisymmetric frames, our predictions show excellent agreement with a recent theory established by Alimov et al. [Phys. Fluids 33, 052104 (2021)]. Moreover, we put in evidence the intriguing capacity of minimal surfaces between nonaxisymmetric frames to transmit a mechanical torque despite being completely liquid. These forces could be interesting to exploit for mechanical self-assembly of soft matter systems or as highly sensitive force captors.